Vertiefung II

pH - Berechnungen  - Herleitung der Näherungsformeln

1. Starke Säuren / Basen
Starke Säuren und Basen dissoziieren praktisch vollständig: HA 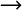H⁺ + A^- (100%) bzw. BOH 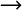B⁺ + OH^- (100%). Die Stoffmengenkonzentration von H⁺ ist damit gleich der Stoffmengenkonzentration der Säure; die Stoffmengenkonzentration von OH^- ist gleich der Stoffmengenkonzentration der Base.
 Aus der Theorie ist bekannt, dass exakt nicht die Stoffmengenkonzentration sondern die "Aktivität" verwendet werden sollte.
Es gilt a = f * c, f = "Aktivitätskoeffizient. Für abschätzende Näherungsrechnungen wird f = 1 benutzt; die Aktivität ist dann gleich der Stoffmengenkonzentration. Als Richtwert gilt, dass für Konzentrationen kleiner als ca. 0,1 mol/l die Näherungsberechnung hinreichend genau ist.
 Aus der Theorie der chemischen Gleichgewichte ist bekannt, dass in Wasser das Produkt der Konzentrationen der H⁺- und der OH^--Ionen einen festen Wert besitzt. (Exakt müssten auch hier wieder die Aktivitäten benutzt werden.)
Dieses "Ionenprodukt des Wassers" K_W = c(H⁺) * c(OH^-) hat den Zahlenwert von ca. 10^-14. (Der genaue Wert ist temperaturabhängig.)
In Analogie zur Definition des pH-Werts, pH = - log( c(H⁺) ), wurde logarithmisch der pK-Wert definiert: pK_W = - log( K_W ) = 14; ebenso wurde definiert: pOH = - log( c(OH^-) ). Für Basen gilt c(H⁺) = K_W / c(OH^-); logarithmiert pH = pK_W - pOH = 14 - pOH.

2. Schwache Säuren
Schwache Säuren dissoziieren nicht vollständig: HA 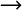H⁺ + A^- ( <100%). In einer wässrigen Lösung einer schwachen Säure HA kommen daher alle 3 Teilchensorten vor - HA, H⁺ und A^-. Auch dafür ist aus der Theorie der chemischen Gleichgewichte ein wichtiges Ergebnis bekannt: Die Konzentrationen der drei Teilchensorten hängen über eine "Gleichgewichtskonstante" K zusammen! Für Säuren benutzt man häufig auch die Namen "Dissoziationskonstante" oder "Säurekonstante" und verwendet das Symbol K_S bzw. die logarithmierte Größe pK_S = - log( K_S ). Die Theorie gibt auch an, wie dieser Zusammenhang aussieht: "Konzentrationen der Produkte" / "Konzentrationen der Edukte". (Ganz genau müssten auch dabei wieder die "Aktivitäten" verwendet werden.)
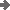 Für HA 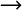H⁺ + A^- gilt: K_S = c(H⁺) * c(A^-) / c(HA).
Wenn eine Säure HA dissoziiert (d.h. in die anderen Teilchen H⁺ und A^- zerfällt), zeigt die Reaktionsgleichung, dass gleich viele H⁺ und A^- entstehen. Damit ist c(H⁺) = c(A^-). Es gilt dann auch K_S = c(H⁺)² / c(HA). ("GLEICHUNG A")
c(HA) ist die Konzentration der nach (!) dem Zerfall in der Lösung vorhandenen nicht dissoziierten HA-Teilchen. Wenn c_S die Konzentration der Säure vor (!) der Dissoziation ist, gilt c(HA) =c_S - c(H⁺). (Für jedes gebildete H⁺ und A^- ist ein HA weniger vorhanden.)
Daraus folgt: K_S = c(H⁺)² / [ c_S - c(H⁺) ].
Aufgelöst ist dies eine quadratische Gleichung für c(H⁺): c(H⁺)² + K_S*c(H⁺) - K_S*c_S = 0.
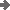   Man kann die Sache noch weiter komplizieren: Auch Wasser dissoziiert! Damit enthält eine Lösung einer Säure HA neben H₂O-Molekülen die Teilchen HA, H⁺, A^- und OH^-. H⁺ und OH^- sind über K_W miteinander verknüpft. Auch dies ist über die Theorie der chemischen Gleichgewichte berechenbar.
Es entsteht dann die noch kompliziertere Formel: c(H⁺) - K_W / c(H⁺) - K_S*c_S / [ K_S + c(H⁺) ] = 0.
(Aufgelöst eine Gleichung dritten Grades für c(H⁺)!) ("GLEICHUNG B")
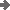 Anstelle sich mit diesen Formeln herumzuschlagen, führt man eine Näherung ein: Schwache Säuren dissoziieren gering (Richtwert = einige %). Damit ist die Konzentration der in der Lösung vorhandenen undissoziierten Teilchen HA praktisch gleich der Konzentration der gesamten Säure c_S.
"Gleichung A" wird damit einfacher: K_S = c(H⁺)² / c_S; aufgelöst c(H⁺)² = K_S * c_S bzw. c(H⁺) = [ K_S * c_S ]^1/2.
Dies ist die vorher angegebene Formel. Logarithmiert entsteht daraus die angegebene "alternative Formel".

3. Schwache Basen
Für schwache Basen gelten genau dieselben Überlegungen!
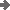 Für die Dissoziation BOH 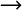B⁺ + OH^- wird eine Basenkonstante K_B = c(B⁺) * c(OH^-) / c(BOH) eingeführt. Die weiteren Ableitungen sind analog, wenn c(H⁺) durch c(OH^-), c_S durch c_B und K_S durch K_B ersetzt werden!
Es folgt die angegebene Näherungsformel c(OH^-) = [ K_B * c_B ]^1/2 und deren logarithmierte "alternative Formel".
Der pH-Wert wird mit pH = 14 - pOH errechnet.
 Der Vorteil dieses Wegs über OH^- ist, dass gleichartige Ableitungen und Formeln wie für die Säure benutzt werden. Ein Weg über die zu einer Base "konjugierte Säure" ist prinzipiell auch möglich, bietet aber keine Vorteile. (Unterrichtserfahrung: meistens werden dann falsche Formeln hergeleitet!)

4. Gültigkeit der Näherungsformeln für schwache Säuren/Basen
Die Näherungsformel ist dann gut benutzbar, wenn für die Zahlenwerte gilt: c_S > 100 * K_S (bzw. c_B > 100 K_B).
Als Beispiel einige Ergebnisse für Essigsäure (pK_S = 4,75; K_S  = 1,778*10^-5).

Bei 10^-3 mol/l ist die Näherungsformel noch gut brauchbar (0,7 % Abweichung); im Bereich von K_S ist die Abweichung deutlich (5,3 %); die scheinbar "bessere" Formel, die quadratische Gleichung A, liefert völlig  falsche Resultate bei c_S < K_S / 100.

ZURÜCK:    Einführung Formeln für die pH-Berechnung