Vertiefung III
pH - Berechnungen -
Mehrwertige Säuren
Mehrwertige Säuren
Die
Überlegungen für mehrwertige Basen sind analog, wenn die in "Vertiefendes
Material II" genannten Ersetzungen { c(H+) durch c(OH-),
cS durch cB und KS durch KB } durchgeführt
werden.
Mehrwertige Säuren können stufenweise H+ abgeben. Die erste
Dissoziationsstufe kann dabei zum Typ "starke Säure" gehören
- Beispiel Schwefelsäure. die weiteren Dissoziationsstufen gehören
praktisch immer zum Typ "schwache Säure". Die beste Möglichkeit
ist, alle in der Lösung vorkommenden Teilchensorten zu berücksichtigen;
das führt aber natürlich zu umständlichen Gleichungen. Teilweise
lassen sich "mit chemischen Überlegungen" Näherungen einführen.
 Wir betrachten das Beispiel Schwefelsäure,
cS = 0,01 mol/l.
Wir betrachten das Beispiel Schwefelsäure,
cS = 0,01 mol/l.
|
1. Stufe
|
H2SO4 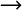 HSO4- + H+
HSO4- + H+
|
praktisch 100 % - starke Säure
|
|
2. Stufe
|
HSO4- 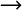 SO42- + H+
SO42- + H+
|
Gleichgewicht, pKS = 1,92 - schwache Säure
|
Die Berechnung der Gleichgewichte (alle Teilchensorten) führt zu folgender
Lösung:
pH = 1,838; c(H2SO4) = 7,9*10-8
(0%); c(HSO4-) = 5,5*10-3 (55%); c(SO42-)
= 4,5*10-3 (45%).
 Falsch wäre eine Rechnung: cS = 0,01; pH = - log(
cS ) = 2. (Nur die erste Stufe berücksichtigt)
Falsch wäre eine Rechnung: cS = 0,01; pH = - log(
cS ) = 2. (Nur die erste Stufe berücksichtigt)
 Auch falsch ist eine Rechnung: Schwefelsäure ist zweiwertig,
1 H2SO4 liefert also 2 H+;
Auch falsch ist eine Rechnung: Schwefelsäure ist zweiwertig,
1 H2SO4 liefert also 2 H+;
für cS
= 0,01 ist demnach c( H+ ) = 2 * cS = 0,02; pH = - log(
0,02 ) = 1,699.
 Eine richtige Lösung mit "chemischen Überlegungen"
wäre:
Eine richtige Lösung mit "chemischen Überlegungen"
wäre:
Die 1. Dissoziationsstufe verläuft vollständig; 0,01
mol/l H2SO4 liefern also 0,01 mol/l H+ und
0,01 mol/l HSO4-.
Für die 2. Stufe haben wir ein
Gleichgewicht: KS = 10-1,92 = 0,01202 = c( H+
) * c( SO42- ) / c( HSO4- ).
Wenn
ein Anteil x von HSO4- dissoziiert: es entstehen x SO42-,
c( HSO4- ) = 0,01 nimmt um x ab
und c( H+
) = 0,01 nimmt um x zu: KS = [ 0,01 + x ] * x / [ 0,01 - x ]
Die
(positive) Lösung der quadratischen Gleichung x2 + ( 0,01 +
KS ) * x - KS * 0,01 = 0 ist: x = 0,004528.
Daraus folgt
das Ergebnis: c( H+ ) = 0,014528; pH = 1,838; c( HSO4-)
= 5,5*10-3; c( SO42- ) = 4,5*10-3.
|

|
Schon dieses - noch einfache - Beispiel zeigt,
dass "umständliche" Rechnungen nötig sind.
Noch
"verwirrender" sind Fälle mit mehreren Dissoziationsstufen,
die alle "schwach" sind, Beispiel Phosphorsäure!
|
Beispiel Phosphorsäure, cS = 0,01
mol/l.
Aus "chemischen Überlegungen" erwarten wir,
dass die 3. Dissoziationsstufe keine Bedeutung besitzt, dass also praktisch
kein PO43- vorkommt. Wieviel von den anderen Teilchensorten
vorkommt, lässt sich schwer erraten; wahrscheinlich ist auch wenig aus
der zweiten Dissoziationsstufe kommendes HPO42- vorhanden.
Die pH-Berechnung könnte eventuell umständlich sein, da miteinander
verknüpfte Gleichgewichte vorkommen.
Die Lösung ist unter
Verwendung der pKS-Werte 2,10; 7,00; 11,35:
pH = 2,24;
42% H3PO4 und 58% H2PO4-
und wie erwartet praktisch kein HPO42- und PO43-
Das
Ergebnis zeigt, dass wegen der stark unterschiedlichen pKS-Werte
nur die 1. Dissoziationsstufe wichtig ist.
{Wenn man mit pKS
= 2,1 als 1-wertige Säure mit der Näherungsformel rechnet: pH = 2,05
(8% Abweichung vom richtigen Wert)}
|

|
Nur durch Berechung aller Gleichgewichte lässt
sich ein Fall mit 4 Dissoziationsstufen behandeln.
Beispiel EDTA
als Säure (HOOC - CH2 - )2 - N - CH2
- CH2 - N - (CH2 - COOH)2
(dafür
wird die Abkürzung H4Y benutzt):
|
Beispiel EDTA als 4-wertige
Säure mit den pKS-Werten 2,1; 2,7; 6,2; 10,3 - cS
= 0,01 mol/l.
Aus "chemischen Überlegungen" erwarten
wir in einer sauren Lösung wenig Produkte aus den Dissoziationsstufen mit
pKS = 6,2 und 10,3; es sollte also wenig Y4- und HY3-
vorkommen. Die ersten zwei Dissoziationsstufen haben ähnliche pKS-Werte,
es sollten also H4Y, H3Y- und H2Y2-
vorkommen.
Die Lösung ist: pH = 2,15; 41 % H4Y;
46% H3Y- und 13% H2Y2- und praktisch
kein HY3- und Y4-.
{Mit "chemischen
Überlegungen" kommt man wohl nie zu dieser Lösung! Hier ist ein
"Programm", das alle Dissoziationsgleichgewichte berechnet, der einzig
sinnvolle Weg!}
|

|
SCHLUSSFOLGERUNG:
Nur mit "Papier und
Bleistift" lässt man von solchen Rechnungen die Finger
weg!
Dafür benutzt man besser "Programme"!
|
ZURÜCK: Einführung
Formeln für die pH-Berechnung