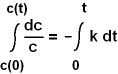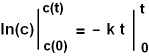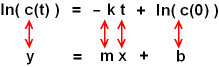Startpunkt ist die differentielle Geschwindigkeitsgleichung. Diese ist Ergebnis
von Versuchen: Es wurde gefunden, dass für eine Reihe chemischer Reaktionen
die Geschwindigkeit proportional zur Konzentration des Ausgangsstoffs ist.
|
In der Differentialrechnung ist die Geschwindigkeit als Differentialquotient
definiert.
k wird eingeführt, um aus der Proportionalität
eine Gleichung zu erzeugen.
k enthält die Charakteristik
der speziellen Reaktion und die Temperatur.
Das Minus-Vorzeichen
wird eingeführt, weil c die Konzentration eines Ausgangsstoffs
ist,
und dessen Konzentration nimmt mit fortlaufender Reaktionszeit
ab.
|
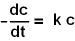
|
Um diese "Differentialgleichung" zu lösen, benutzt man das
Verfahren der "Separation der Variablen".
|
Wir bringen alle Teile mit der Variable c auf die linke Seite.
|
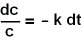
|
Nun ist auf beiden Seiten eine Integration möglich. Entweder wird zuerst
unbestimmt integriert und die Integrationskonstanten werden dann über die Anfangs-
und Randbedingung festgelegt. Einfacher ist auf beiden Seiten in zueinander
passenden ("korrespondierenden") Grenzen bestimmt zu integrieren.
Am Beginn der Reaktion haben wir die Zeit t = 0 und die Anfangskonzentration
c(0). Zu einem späteren Zeitpunkt t haben wir die dann noch vorhandene
Konzentration c(t).
{Lassen Sie sich nicht verwirren! Es ist
in solchen Herleitungen zur chemischen Kinetik üblich, für die Integrationsvariable
(in dt) und die Reaktionszeit (t in den Integrationsgrenzen) denselben Buchstaben
zu benutzen.}
|
Beide Seiten werden integriert.
|
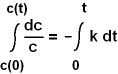
|
|
|
|
Die Lösung der Integrationen ist:
|
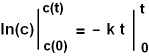
|
ausgewertet:
|
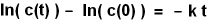
|
Durch Vergleich mit der allgemeinen Geradengleichung (Steigungsform) "y
= mx + b" sehen wir, bei einer Auftragung ln(c) als y und t als x:
|
Eine Gerade mit der Steigung - k und dem Achsenabschnitt ln(
c(0) ).
|
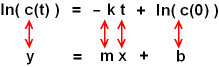
|
Die Lösung mit Logarithmen kann mit der
Identität
"ln( a / b) = ln(a) - ln(b)" umgeformt
werden.
|
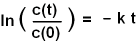
|
Entlogarithmiert folgt:
|
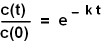
|
Für die Halbwertszeit benutzen wir die Definition: Nach einem Zeitintervall
t1/2 liegt noch die halbe Konzentration einer Anfangskonzentration
c(0) vor, also c(t1/2) = c(0) / 2. Das Ergebnis der Rechnung bestätigt
dann die Behauptung, dass t1/2 nicht von der Anfangskonzentration
abhängt; d.h. der Zeitnullpunkt kann beliebig gewählt werden.
{Bei
Reaktionen anderer als der 1. Ordnung gilt das nicht mehr! Dann hängt t1/2
von c ab!}
|
In der logarithmierten Form setzen wir
diese
Bedingung ein:
|
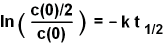
|
Mit der Identität
"ln(1/2) = - ln(2)"
folgt:
|
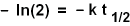
|
|

|
ZURÜCK - Geschwindigkeitsgesetz
|
![]()