In allen Beispielen wird die Formel für 25 °C mit dem dekadischen Logarithmus benutzt.

Zuerst Beispiele zum (rechnerischen) Umgang mit der Nernstschen Gleichung

1) Welches Einzelpotential hat eine Halbzelle Ag | Ag⁺ (a = 0,05)?
E_o = + 0,800 V; z = 1; E = +0,800 + 0,0592 / 1 * log(0,05) = +0,723 V.

2) Welches Einzelpotential hat eine Halbzelle Ca | Ca²⁺ (a = 0,3)?
E_o = -2,866 V; z = 2; E = -2,866 + 0,0592 / 2 * log(0,3) = -2,881 V.

3) Welche EMK hat eine Zelle | Mg | Mg²⁺ (a=1,5) || Al³⁺ (a=0,08) | Al |?
Zuerst Berechnung der Einzelpotentiale, dann EMK = E(positiver) - E(negativer).
Bei richtig geschriebenem Symbol ist das auch: EMK = E(rechts) - E(links).
E("Mg") = -2,363 + 0,0592 / 2 * log(1,5) = -2,358 V
E("Al") = -1,662 + 0,0592 / 3 *  log(0,08) = -1,684 V
EMK = E("Al") - E("Mg") = 0,674 V

4) Für welche Aktivität a_X ist das Einzelpotential der Halbzelle Ag | Ag⁺ (a_X) 672 mV?
Die Umkehrfunktion des dekadischen Logarithmus log(x) ist die Potenz 10^x.
0,0592 / z * log(a) = E - E_o; log(a) = {E - E_o} * z / 0,0592; a = "10 hoch letzter Ausdruck";
log(a_X) = {+0,672 - (+0,800)} * 1  / 0,0592 = -2,162; a_X = 10^-2,162 =0,00688 ~ 0,0069 (mol/l)

5) Für welche Aktivität a_X ist die EMK der Zelle | Mg | Mg²⁺ (a=0,1) || Al³⁺ (a_X) | Al | 705 mV?
    Runden Sie das Zwischenergebnis E("Mg-Halbzelle") auf 1 mV.
E("Mg") = -2,363 + 0,0592 / 2 * log(0,1) = -2,393 V
EMK = E("Al") - E("Mg"); E("Al") = EMK + E("Mg") = 0,705 + (-2,393) = -1,688 V
log(a_X) = {-1,688 - (-1,662) }* 3 / 0,0592 = -1,318; a_X = 10^-1,318 = 0,0481 ~ 0,048 (mol/l)
{Ohne Rundung ist E("Mg") = -2,3926; EMK = -1,6876; log(a_X) = -1,29729...; a_X = 0,0504}

Beispiele zur Anwendung auf die Vorhersage erwarteter chemischer Reaktionen

6) Welche chemische Reaktion ist zwischen den Paaren Zn | Zn²⁺ (a = 2) und Cr | Cr³⁺ (a = 0,001) zu erwarten?
E("Zn") = -0,763 + 0,0592 / 2 * log(2) = -0,754 V
E("Cr") = -0,744 + 0,0592 / 3 * log(0,001) = -0,803 V
Für die E_o-Werte ist "Cr" positiver als "Zn", die Reaktion Chrom(III) oxidiert Zink zu Zink(II) ist zu erwarten.
Für die E-Werte ist "Zn" positiver als "Cr", die Reaktion Zink(II) oxidiert Chrom zu Chrom(III) ist zu erwarten.
{3 Zn²⁺ + 2 Cr 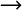3 Zn + 2 Cr³⁺}
Durch verschiedene Konzentrationen bzw. Aktivitäten können die Potentiale so verschoben werden, dass aus
E und E_o verschiedene Aussagen zum erwarteten Reaktionsablauf folgen!

7) Gegeben sind die Paare Sn | Sn²⁺ (a =1) und Pb | Pb²⁺(a_X). Welche Reaktion läuft ab, wenn a_X = 1?
    Welche Aktivität a_X muss vorliegen - mindestens oder höchstens - damit sich der Reaktionsablauf umkehrt?
Standardpotentiale: "Sn" -0,140 V; "Pb" -0,126 V. E_o von Pb ist positiver, also findet bei "Pb" die Reduktion statt.
Wenn a_X = 1: Pb²⁺ oxidiert Sn zu Sn²⁺ (und wird dabei zu Pb reduziert).
{Pb²⁺ + Sn 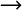Pb + Sn²⁺}
Für Sn ist a = 1, also E = E_o. Damit die umgekehrte Reaktion abläuft, muss das Potential von "Pb" so weit nach links
verschoben werden, dass es negativer als das Potential von "Sn" wird. Eine Verschiebung nach links ist nach der
Nernstschen Gleichung möglich, wenn a < 1. (Dann ist log(a) < 0, also wird eine negative Zahl zu E_o addiert.)
Die mindestens nötige Verschiebung nach links ist erreicht, wenn E("Pb") = E("Sn"). Die dann berechnete Aktivität a_X
ist also die höchst mögliche Aktivität für den verlangten "umgekehrten" Reaktionsablauf.
E ("Pb") = E_o("Pb) + 0,0592 / 2 * log(a_X): log(a_X) = {-0,140 - (-0,126) } * 2 / 0,0592 = -0,473; a_X = 0,34.
Wenn a_X < 0,34 oxidiert Sn²⁺ Pb zu Pb²⁺ (und wird dabei zu Sn reduziert).
{Sn²⁺ + Pb 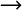Sn + Pb²⁺}

8) (Verständnisfrage - nach den bisherigen Beispielen lösbar): Durch geeignete Aktivitäten wird erreicht, dass zwei
     Paare Metall | Metallion trotz verschiedenem E_o das gleiche E besitzen. Welche Aussage zur Reaktion folgt daraus?
Bisher haben wird gesehen: Beim edleren Paar mit dem positiveren E findet die Reduktion statt. Bei gleichem E ist dann also
keines der Paare edler. Es wird keine Reaktion stattfinden.
Präzise drückt man das so aus: Die Reaktion befindet sich im Gleichgewicht.

9) Verständnisfrage: Wir gehen von den Halbzelle Cu | Cu²⁺ (a=1) und Zn | Zn²⁺ (a=1) aus.
     Wie verändern sich im Laufe der dann möglichen Reaktion die beiden Einzelpotentiale und die EMK?
Am Anfang gelten die Standardpotentiale (+0,342 und -0,763 V).
Dafür ist - wie inzwischen sicher sofort lösbar (!) - die Reaktion: Cu²⁺ oxidiert Zn zu Zn²⁺.
Reaktionsgleichung: Cu²⁺ + Zn 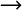Cu + Zn²⁺.
Die Cu²⁺-Aktivität nimmt also ab und die Zn²⁺-Aktivität nimmt zu. Für die Potentiale E gilt daher:
E("Cu") wird kleiner (weil a kleiner wird) und E("Zn") wird größer.
Da nun beide Potentiale E näher aneinander rücken, wird die Differenz der beiden kleiner: die EMK wird kleiner.
{Allgemeinere Zusatzüberlegung: Beim Ablauf der Reaktion wird sich schließlich als Endzustand das Gleichgewicht
  einstellen. Dafür ist die EMK = 0; die anfängliche EMK = 1,105 V muss also kleiner werden.}