Kovalente Bindung

Ausgehend von der VB-Theorie ("Valence Bond") kann die Bindung qualitativ erklärt werden: Die Orbitale der Atome überlappen sich, und diese Überlappung führt zu einem Energiegewinn. In den Strichformeln entspricht einer solchen Überlappung der Bindungstrich. Mit den aus der Atomtheorie bekannten Atomorbitalen (AO) lassen sich nicht alle experimentell bekannten Geometrien beschreiben. Dann bildet man an einem Atom Kombinationen der AO; die so entstehenden Hybridorbitale können dann mit Orbitalen des Nachbaratoms überlappen. In den Strichformeln wird auch dafür ein Bindungsstrich geschrieben. Wir betrachten hier s- und p-Orbitale und Hybridorbitale dazu. (Unter Verwendung von d-Orbitalen lassen sich noch viele andere als die hier besprochenen Geometrien von Molekülen beschreiben.)

Zur Einführung sehen wir uns das Wasserstoffmolekül H₂ an. Mit Strichformeln schreiben wir: H - H.
Im H-Atom liegt ein 1s-Orbital vor, dafür kann (im Modell von Schrödinger) eine Kugel um den Atomkern gezeichnet werden.

Warum gibt es keine weiteren Überlappungsmöglichkeiten?
Die Antwort darauf ist ein wenig schwieriger! Bisher haben wir nicht berücksichtigt, dass Orbitale einer Funktion entsprechen, die auch ein Vorzeichen hat. Bei einer Überlappung bilden wir das Produkt beider Funktionen, also auch das Produkt der Vorzeichen. Wenn mehrere Teilzonen vorliegen, müssen die Überlappungszonen unter Berücksichtigung des Vorzeichens addiert werden. Dabei kann der Fall auftreten, dass sich die Teilflächen - gleicher Betrag aber verschiedenes Vorzeichen - kürzen.
(Mathematisch entspricht die Flächenbildung einer Integration.)
WICHTIG: Diese Vorzeichen nicht mit der Ladung verwechseln!

Wir konstruieren nun 2 Situationen, die scheinbar eine Überlappung liefern, aber bei denen sich die Teilzonen unter Berücksichtigung der Vorzeichen kürzen. Insgesamt entsteht damit kein Energiegewinn; also führt dies auch nicht zu einer Bindung!

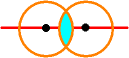
Wenn sich 2 1s-Orbitale nähern, entsteht in der Mitte eine Überlappungszone. (Räumlich ist das eine Schnittfigur - wie der Raum zwischen zwei übereinander gelegten Uhrgläsern.)
Die Überlappungszone liegt in der Kernverbindungslinie, man nennt dann die so entstehende Bindung eine s-Bindung. (Ähnlich wie s-, p- d- usw. die Form eines AO beschreiben, beschreiben die griechischen Buchstaben die Form der Überlappung.) Insgesamt gehören die 2 Elektronen der H-Atome nun beiden gemeinsam. (In der Überlappungszone ist die Aufenthaltswahrscheinlichkeit am größten.) 2 Elektronen halten die beiden Atome zusammen, es liegt eine Elektronenpaarbindung vor. Dafür wird in der Formelschreibweise der Bindungsstrich geschrieben.
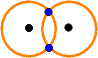
Im alten "primitiven" Bild gehören die Elektronen zu beiden Bahnen. (Die Zeichnung zeigt, dass das alte Bild die Überlappung auch schon "primitiv" enthalten hat.)

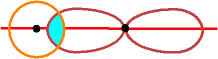
s mit p Die Überlappung führt zu einer s-Bindung, weil die Überlappungszone in der Kernverbindungslinie liegt.
p mit p - 1. Möglichkeit Wieder eine s-Bindung
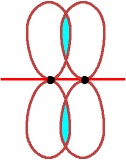
p mit p - 2. Möglichkeit Die Überlappung (2 Teilzonen) findet außerhalb der Kernverbindungslinie statt. Dies nennt man eine p-Bindung.

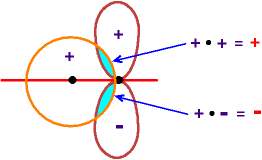
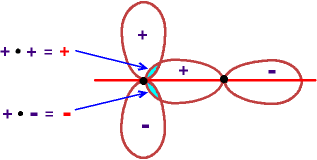
s mit p "2. Möglichkeit"		p mit p "3. Möglichkeit"
Die beiden Teilzonen der Überlappung haben jeweils gleiche Fläche aber verschiedenes Vorzeichen, insgesamt entsteht so keine Überlappung.