HYBRIDISIERUNG
|

|
Die Anwendung des Konzepts, dass eine Bindung durch eine Überlappung
von Atomorbitalen entsteht, führt zu Widersprüchen: Die
experimentell bekannten Geometrien von Molekülen und auch deren
Bindungsverhältnisse lassen sich nicht beschreiben!
Die
drei p-Orbitale haben Winkel von 90° zueinander, also können
auch verschiedene Partner nur unter diesem Winkel gebunden werden.
In der Natur treten aber z.B. beim C-Atom Bindungswinkel von 120°
(Ebene) und 109,5° (räumlich, Tetraeder) auf!
Die C
= C Doppelbindung ist mit Atomorbitalen nicht zu verstehen!
Linus
Pauling hat entdeckt, dass dieses Problem durch geeignete Kombinationen
von Atomorbitalen lösbar ist.
|
Wir betrachten die Kombination zwischen s- und p-Orbitalen.
(Damit
lassen sich die Verbindungen der organischen Chemie beschreiben; d-Orbitale
werden in komplizierteren Strukturen der Anorganischen Chemie benötigt.)
Ein s- und ein p-Orbital:
Die Kombination
liefert zwei neue Hybridorbitale. Auch für diese gilt das
Pauli-Prinzip: ein Hybridorbital kann mit maximal 2 Elektronen besetzt werden.
Die Orbitale werden "nach der Entstehungsgeschichte" als sp-Orbitale
bezeichnet. (Dies war sinnvoller, als weitere neue Buchstaben einzuführen!)
|

|
+
|

|
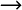
|

|
|
s-Orbital
|
|
p-Orbital
|
|
2 sp-Orbitale
|
Ein s- und zwei p-Orbitale:
Die Kombination
liefert drei neue Hybridorbitale, die wieder "nach der Entstehungsgeschichte"
sp2-Orbitale bezeichnet werden. Interessant ist, dass zwischen
den drei Hybridorbitalen ein Winkel von 120° vorliegt. Offenkundig lassen
sich jetzt Verbindungen mit einem Bindungswinkel zu den Nachbarn von 120°
auch beschreiben! Die drei Orbitale liegen in einer Ebene.
|

|
+
|

|
+
|

|
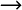
|

|
|
s-Orbital
|
|
p-Orbital (px)
|
|
p-Orbital (py)
|
|
3 sp2-Orbitale
|
|
Oft zeichnet man zur Vereinfachung
nur den
größeren Teil des Hybridorbitals
|

|
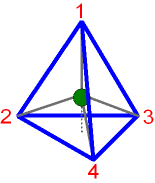
Ein s- und drei p-Orbitale:
Die Kombination
liefert vier neue Hybridorbitale, die als sp3-Orbitale
bezeichnet werden. Die Orbitale sind räumlich in Richtung der Tetraederecken
angeordnet, und zwischen den Orbitalen liegt ein Winkel von 109,5° vor.
(Tetraeder = räumliche Figur, aufgebaut aus 4 gleichseitigen Dreiecken)
|
|
|
|
Um die Mitte des Tetraeders sind 4 Eckpunkte symmetrisch
angeordnet.
Die Winkel zwischen den Verbindungslinien
Mitte
zum Eckpunkt sind jeweils 109,5°
("Tetraederwinkel")
|
Meist zeichnet man dafür eine ebene
Projektion.
In
dieser sind dann die Winkel
zwischen den Verbindungslinien 90°.
|
| 
|
+
|

|
+
|

|
+
|

|
|

|
| s-Orbital
|
|
p-Orbital (px)
|
|
p-Orbital (py)
|
|
p-Orbital (pz)
|
|
4 sp3-Orbitale
|
Auch hier zeichnet man oft zur Vereinfachung nur den größeren
Teil des Hybridorbitals.
Anmerkungen zum Verständnis:
1. Die "Schorle"-Erklärung:
Wieviele Hybridorbitale entstehen?
Wenn wir 1 Glas Apfelsaft mit 2 Gläsern Mineralwasser mischen, entstehen
... ? Natürlich haben wir hinterher 3 Gläser des Mischgetränks
"Schorle" - ein "Hybridgetränk" aus Apfelsaft und Mineralwasser. (Pfälzer dürfen anstelle von Apfelsaft auch Wein
verwenden!) Das Beispiel zeigt auch noch: Es ist etwas neues entstanden, in
der "Entstehungsgeschichte" sind die beiden alten Arten enthalten.
Wie Apfelsaft und Mineralwasser ist Schorle ein Getränk - also wie das
s- und das p-Atomorbital sind die beiden sp-Orbitale Atomorbitale.
|
|

|

|

|

|

|

|
|
|
1 Glas A und 2
Gläser M
|
3 Gläser SM-Hybrid
|
Diese Erklärung beschreibt einen Sachverhalt gut:
Die Mischung
(das Hybridorbital) ist etwas neues, hängt aber mit den Ausgangs-Atomorbitalen
zusammen. Ein s-Atomorbital hat zu 100% s-Charakter, ein p-Atomorbital zu 100%
p-Charakter, ein sp3-Hybridorbital hat zu 25% s- und zu 75% p-Charakter. Das
Hybridorbital ist eine mathematische Mischung aus den Atomorbitalen.
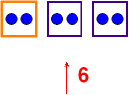
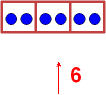
2. Elektronen-Bilanz:
Wenn wird drei Atomorbitale mischen, die insgesamt
6 Elektronen aufnehmen können, dann ...? Nach der Kombination muss auch
Platz für genau 6 Elektronen sein; weil 1 Orbital 2 Elektronen aufnehmen
kann, sind 3 Hybridorbitale nötig!
|
|
|
|
|
|
3 Atomorbitale
|
3 Hybridorbitale
|
|
|
Beide haben Platz
für 6 Elektronen
|
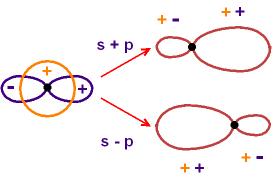
3. Etwas "mathematischer":
Wir bilden aus einem s- und einem
p-Orbital zwei Kombinationen: s + p und s - p.
Die Skizze zeigt, dass (vereinfacht
gezeichnet!) zwei sp-Orbitale entstehen; bei gleichem Vorzeichen addiert sich
der Funktionswert, bei verschiedenem Vorzeichen kürzen sich die Funktionswerte
teilweise. (Die genauere Form der Orbitale folgt aus der "richtigen"
theoretischen Rechnung.)
Die beiden Atomorbitale s und p wurden "linear kombiniert",
um zwei neue Hybridorbitale zu erzeugen.
Analog geht man für den Fall sp2 und sp3
vor, die Theorie ergibt dann, welche lineare Kombination zu wählen ist.
Für sp3 sind die 4 Kombinationen, die die gewünschte Geometrie
- in Richtung Tetraderecken - liefern:
|
|
s
|
+
|
px
|
+
|
py
|
+
|
pz
|
|
|
s
|
+
|
px
|
-
|
py
|
-
|
pz
|
|
|
s
|
-
|
px
|
+
|
py
|
-
|
pz
|
|
|
s
|
-
|
px
|
-
|
py
|
+
|
pz
|
Wir sehen, dass auch hier die Atomorbitale mit geeigneten Vorzeichen
in linearen Gleichungen neu "zusammen kombiniert" wurden. Hybridisierung
bedeutet also ein "mathematisches Mischen".
4. Zum Tetraeder und zum Tetraederwinkel:
|
Bei Interesse finden hier Sie eine Skizze zur
Tetraedergeometrie
und eine rechnerische Herleitung des Tetraederwinkels.
|

|
5. Gibt es auch andere Hybridisierungen?
|
Für s- und p-Orbitale: nein
Mit d-Orbitalen
sind auch weitere Geometrien möglich!
|

|
WEITER: Hybridisierung
am C-Atom ZURÜCK: Anfang
"Kovalente Bindung"
![]()