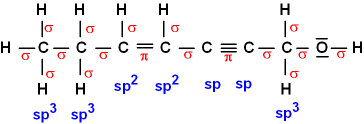LÖSUNGEN - "Kovalente Bindung"

A

1. Mit der Hybridisierung kann man die tatsächlich in der Natur vorkommenden Bindungsverhältnisse beschreiben. Vor allem die Geometrie vieler Moleküle (Tetraderwinkel und 120° bei Doppelbindungen) kann ohne Hybridisierung nicht erklärt werden! Erst mit der Hybridisierung ist der Aufbau von Doppel- und Dreifachbindungen verständlich.
2. Um die richtigen Kombinationen der Atomorbitale zu bilden und dann diese mit jeweils 1 Elektron zu besetzen, ist die "Promotion" am C-Atom nötig. Dabei wird ausgehend vom Grundzustand ein gedachter (keine realer!) angeregter (also Zustand höherer Energie) Zwischenzustand angenommen, von dem aus die Hybridisierung abgeleitet wird. Jedes der dann besetzen Orbitale bildet mit Elektronen des Partner Elektronen-Paar-Bindungen. Für die Bildung des promovierten Zustands ist eine Energie nötig, die Bildung des Moleküls liefert einen größeren Energiegewinn.
3. Mathematisch werden Summen bzw. Differenzen der Atomorbitale gebildet. Wie diese linearen Gleichungen aussehen, hat Linus Pauling erforscht. Die Hybridorbitale sind immer noch Atomorbitale; sie werden aber erst zur Erklärung der chemischen Bindung eingeführt und nicht schon zur Erklärung des Atombaus. Weil Elektronen nicht verschwinden oder aus dem Nichts erzeugt werden können, gibt es immer gleichviele kombinierte Hybridorbitale wie Atomorbitale zur Hybridisierung benutzt wurden. Hybridorbitale zeigen räumlich in andere Richtungen als die zugrunde gelegten Atomorbitale. Wegen der größeren Ausdehnung in einer Richtung (Form der Doppelkeule beachten!) ist eine besssere Überlappung mit Nachbarorbitalen möglich.
4. Nur bei der Doppelbindung.
5. Freie Drehbarkeit besteht dann, wenn die Drehung nichts an der Überlappung ändert. Die Überlappung ist der Grund, dass sich eine kovalente Bindung ausbildet. Bei einer C - C - Bindung liegt die Überlappungszone in der Kernverbindungslinie, es kann also um diese Linie herum gedreht werden. Anders als bei dieser s-Bindung enthält die C = C - Doppelbindung auch eine p-Bindung. Dabei überlappen die p-Orbitale in 2 Teilzonen außerhalb der Kernverbindungslinie. Eine Drehung würde diese Überlappung aufheben. Dieser Bruch der p-Bindung ist nur durch Energiezufuhr möglich.
   
   ---- Zurück zum Aufgabentext
    
6. Nein - nur 1 Überlappung. Zum Verständnis: 1 p-Orbital hat auch 2 Hälften. Ebenso tritt bei der Seite an Seite Überlappung diese an 2 Hälften auf, insgesamt ist es nur 1 Überlappung der zwei Orbitale.
7. H mit H: H besitzt nur das 1s-Orbital. Dieses kann mit einem weiteren H überlappen: 1 s - s.
   C benutzt in Bindungen die Hybridorbitale.
   C mit H: Überlappung mit einem s-Orbital von H, für eine CH-Bindung: 2 sp³ - s (an einer Einfachbindung);
   3 sp² - s (an einer Doppelbindung); 4 sp - s (an einer Dreifachbindung).
   C mit C: 5 sp³ - sp³ (Einfachbindung); 6 sp³ - sp² (Einfachbindung an einer Doppelbindung);
   7 sp³ - sp (Einfachbindung an einer Dreifachbindung); 8 sp² - sp (Doppelbindung an einer Dreifachbindung).
   Zu einer s-Bindung mit einer zusätzlichen p-Bindung führen: a sp² - sp² (Doppelbindung); b sp - sp (Dreifachbindung);
8. Aus der Herleitung der Hybridorbitale ist zu sehen: p-Atomorbitale für p-Bindungen bleiben übrig neben sp²- oder sp-Hybridorbitalen. Eine p-Bindung kommt in Doppel- und Dreifachbindungen vor, muss darum stets zusätzlich die s-Bindung enthalten.
9. Sehen Sie sich die Beispiele an! Eine nicht mögliche Überlappung enthält mehrere Zonen, die sich wegen der Vorzeichen (Produkte der Vorzeichen der Orbitale bzw. Teile davon bei p-Orbitalen) kürzen.
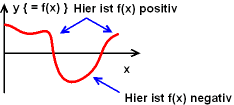
10. Weder Ladungen noch Teilladungen! Das sind die Vorzeichen der Funktion! Natürlich kann man sich das bei dreidimensionalen Funktionen nicht mehr gut vorstellen! Vergleichen Sie die eindimensionale Erklärung:
     
    
    ---- Zurück zum Aufgabentext
     
11. Prinzipiell wäre das möglich, da in der Valenzschale 2s² 2p² die benötigten Elektronen für die einfache Besetzung der Orbitale vom Typ sp² vorhanden sind. Übrig bleibt aber dann ein 2s-Orbital. Das ist im Widerspruch zur Erfahrung, dass die sp²-Hybridisierung in Doppelbindungen vorkommt, man also als übrigbleibendes Orbital ein besetztes p-Orbital benötigt. Falsch wird also die weitere Aussage zur möglichen Bindung des C-Atoms.
12. Bindungen werden durch Elektronen in der Valenzschale erklärt. Die Hybridisierung verändert nur den Charakter dieser an der Bindung beteiligten Valenzelektronen. Die 1s-Elektronen der inneren Schale haben damit nichts zu tun.
13. Korrekte Bindungswinkel wären 109,5° (Einfachbindungen, räumliche Tetraederanordnung ), 120° (Doppelbindung, eben) und 180° (Dreifachbindung, linear). Es ist üblich, dafür vereinfacht linear zu zeichnen.
    
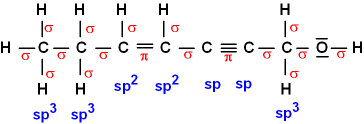
14. Wieder linear gezeichnet:
     
    
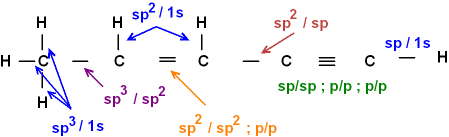
    ---- Zurück zum Aufgabentext 
     

B  

1. Aus dem Aufgabentext ist ersichtlich: Hybridisierung kommt vor. Aus der üblichen Strichformel ist bekannt: es liegen Einfachbindungen vor. Damit kommt nur sp³ in Betracht. Für den Grundzustand ist die Valenzschale von O: 2s² 2p⁴. Wie bei C "promovieren" wir zum angeregten Zustand 2s¹ 2p⁵. Nach Bildung von 4 sp³-Orbitalen haben diese folgende Besetzung: 2, 2, 1, 1. Die beiden einfach besetzten Orbitale bilden nach der Überlappung mit den 1s-Orbitalen von H zwei Einfachbindungen (Elektronenpaarbindung). Übrig bleiben zwei mit 2 Elektronen besetzte sp³-Orbitale. In den Strichformeln werden diese "freien" Elektronenpaare am O dazu gezeichnet.
   
   
   ---- Zurück zum Aufgabentext  
    
2. Wenn NH₃ ein ebenes Molekül wäre, kommt nur ein symmetrisches Dreieck in Betracht. Wegen der Bindungswinkel 120° wäre dann eine sp²-Hybridisierung nötig. Der Grundzustand von N ist in der Valenzschale 2s² 2p³. Nach der Promotion zu 2s¹ 2p⁴ und der Hybridisierung folgen drei einfach besetzte sp²-Orbitale (für die s-Bindung zu den H-Atomen) und ein doppelt besetztes p-Orbital (als freies Orbital). Aber offenkundig will die Natur dieses nicht, auch wenn wir "so schön theoretisch herumgespielt haben"!
   Für eine nicht ebene Struktur von NH₃ ist sp-Hybridisierung unmöglich, da damit nur lineare Moleküle erzeugt werden können, also muss es sp³ sein. Ausgehend von promovierten Zustand 2s¹ 2p⁴ erhalten wir vier sp³-Orbitale mit der Besetzung: 2, 1, 1, 1. Die drei einfach besetzten Orbitale bilden durch die Überlappung mit dem 1s-Orbital von H drei s-Bindungen, das doppelt besetzte sp³-Orbital bleibt als freies Elektronenpaar übrig.
    
   
   ---- Zurück zum Aufgabentext  
    
3. Tetraederstruktur weist auf sp³-Hybridisierung hin. Da ein Kation 1 Elektron weniger hat, ist die Besetzung der vier sp³-Orbitale: 1, 1, 1, 1. Diese Orbitale überlappen jeweils mit 1s-Orbitalen von H unter Bildung von s-Elektronenpaarbindungen.
4. Da sich Methylamin H₃C-NH₂ laut Aufgabenstellung von NH₃ ableitet, muss am N dieselbe Situation vorliegen, also sp³-Hybridisierung. Eine der Überlappungen ist nun nicht mehr sp³ (N) - 1s (H) sondern sp³ (N) - sp³ (C der CH₃-Gruppe).
5. Für ein lineares Molekül ist sp-Hybridisierung nötig. Also (Schritt für Schritt - jeweils für die Valenzschale von C und N):
   Am C: Grundzustand: s² p²; promoviert: s¹ p³; hybridisiert: 2 sp-Orbitale mit je 1 Elektron; 2 p-Orbitale mit je 1 Elektron
   Am N: Grundzustand: s² p³; promoviert: s¹ p⁴; hybridisiert:1 sp-Orbital mit 1 Elektron; 1 sp-Orbital mit 2 Elektronen; 2 p-Orbitale mit je 1 Elektron.
   Nun die Bindung:
   Von C aus: 1 sp (von C) überlappt mit 1s (von H); 1 sp (von C) überlappt mit 1 sp (von N);
   die 2 p-Orbitale (von C) überlappen mit den 2 p-Orbitalen (von N) und vervollständigen die Dreifachbindung zum N
   Von N aus: 1 sp (von N) und 2 p (von N) für die Bindung zum C, übrig bleibt ein doppelt besetztes sp-Orbital am N als freies Elektronenpaar.
    
   
   ---- Zurück zum Aufgabentext 
    
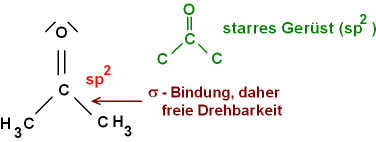
6. Die Doppelbindung am CO bedingt eine sp²-Hybridisierung. Damit ist das Gerüst C - CO - C starr. Die CH₃-Gruppen sind frei drehbar, weil sie über eine s-Bindung (Überlappung von sp³ der Methylgruppe mit sp² am C=O) an C=O gebunden sind.
    
   
    ---- Zurück zum Aufgabentext 

ZURÜCK: Anfang "Kovalente Bindung"