4. Entropie und Freie Enthalpie
|
|
Gibbs und Helmholtz entdeckten,
dass eine neue Größe G ganz allgemein beschreiben kann,
ob ein Prozess möglich ist. In dieser Größe
G ist eine weitere neue Größe S enthalten. Diese kann
nach Entdeckungen von Boltzmann anschaulich interpretiert werden.
|
|
|
Mit
ΔG
kann berechnet werden, ob eine Reaktion
prinzipiell ablaufen kann. Wie schnell dann in der Realität
die Reaktion möglich ist, dazu macht die Theorie keine Aussage.
Die
Geschwindigkeit
chemischer Reaktionen (Kinetik) ist in der Theorie "Thermodynamik"
nicht enthalten!
|
Noch vor der Entwicklung der Thermodynamik bestand ein Interesse, theoretisch
vorherzusagen, ob eine Reaktion ablaufen kann. Ein (besonders misslungener)
Versuch stammt von Berthelot. Seine Theorie
war, dass eine Reaktion exotherm sein muss, damit sie freiwillig ablaufen kann.
"Freiwillig" bedeutet spontan, ohne äußeren Zwang. Eine
Explosion ist dazu ein gutes Beispiel: Unter Gestank, Lärm und Wärmeentwicklung
geschieht die Reaktion freiwillig. Wir kennen einfache Gegenbeispiele: Salze
lösen sich auf und dabei kann es kälter werden. Die "Umgebung"
Lösung musss dem Salz Wärme zuführen, damit es in Lösung
geht. Diese endotherme Reaktion läuft also auch freiwillig ab!
Gibbs und Helmholtz entdeckten, dass H nur ein Teil ist und fanden eine neue
Größe G. Diese wurde "freie
Enthalpie" genannt. Neben H ist eine weitere Größe
S wichtig. Die Entropie S kann thermodynamisch
definiert werden. Für die Interpretation, was in der Natur geschieht, war
die Entdeckung von Boltzmann wichtig, dass die Entropie ein statistisches Maß
für den Ordnungszustand ist. Je größer die Unordnung, desto
größer ist S. Ein Naturgesetz legt fest, dass maximale Unordnung
angestrebt wird. (Dabei ist aber die Art des Systems sehr wichtig!)
Mit diesen beiden Größen S und G lassen
sich Bedingungen formulieren, wie Vorgänge in der Natur ablaufen müssen!
|
Gesetz 1: In einem
abgeschlossenen System sind nur Vorgänge mit ΔS
> 0 möglich.
|
Wenn man dieses Naturgesetz mit Worten beschreibt, bedeutet das: Bei Vorgängen
in der Natur nimmt die Unordnung zu. Im ersten Moment passt dies auch zur Alltagserfahrung.
(Viele Arbeitszimmer und Schreibtische bestätigen das immer wachsende Chaos.)
Aber wir können doch aufräumen, und dann entsteht Ordnung? Der Schlüssel
ist das Wort "abgeschlossen"! Systeme im normalen Leben sind offen!
|
Die geniale Idee von Gibbs war, eine Größe zu finden, die für
jedes System gilt.
Damit sind alle Vorgänge in der Natur beschreibbar.
|
|
Definition
|
G = H - T S bzw. ΔG = ΔH - T ΔS
|
|
Gesetz 2:
|
In der Natur können nur solche Prozesse freiwillig ablaufen,
bei denen ΔG < 0 ist.
|
Anmerkungen:
1. Helmholtz hat eine ähnliche Größe
"Freie Energie" definiert: F = U - T S bzw. ΔF = ΔU - T ΔS
Weil in der Chemie Vorgänge unter konstantem Druck wichtiger sind, wird F bzw.
ΔF in der Chemie selten benutzt.
2. Das
Wort "frei" bezieht sich auf die wichtige Erkenntnis, dass die Energieform
Wärme eine Sonderrolle spielt. Mit G wird die Energie beschrieben, die
auch in anderen Energieformen (z.B. Elektrizität) für den Menschen
frei verfügbar ist.
3. Wenn ΔG = 0,
ist keine Reaktion mehr möglich - dann liegt der Gleichgewichtszustand
vor. Wenn ΔG > 0 ist die Reaktion nicht möglich.
4.
T muss in dieser Gleichung als absolute Temperatur, in K, eingesetzt werden!
Die Gibbsche Gleichung kombiniert (genial) die beiden
Grundtendenzen für Vorgänge in der Natur,
die Energie strebt ein Minimum an,
die Unordnung strebt ein Maximum an!
Mögliche chemische Reaktionen:
Es gilt jeweils: A = Ausgangszustand,
E = Endzustand.
Untersucht
wird jeweils, welche Größen die beiden Teile der Gibbschen Gleichung
haben können, damit insgesamt ΔG
< 0 möglich ist.
|
1
|
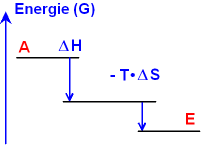
ΔH
< 0 , also eine exotherme Reaktion.
Zusätzlich
ist ΔS >0, die Unordnung
nimmt also zu.
(Beachte: ΔS
> 0 bedeutet - T ΔS
< 0!)
Der Endzustand hat niedrigere Energie als
der Ausgangszustand.
(Dies gilt, wie in der Grafik
sofort zu sehen, auch für ΔS
= 0)
Dies ist der richtige Kern der alten Vorstellung
von Berthelot, dass exotherme Reaktionen freiwillig ablaufen können.
Falsch war, dass nur exotherme Reaktionen möglich sind.
|
|
|
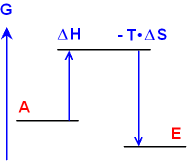
2
|
ΔH > 0, also eine endotherme Reaktion.
ΔG
< 0 ist möglich, wenn
a) der 2. Teil der Gibbschen Gleichung
negativ ist und
b) auch der Betrag des 2. Teils größer
als der des 1. Teil ist.
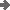( - T ΔS)
< 0 und | T ΔS | > | ΔH
|.
Die Temperatur ist stets positiv;
- ΔS
< 0 bedeutet ΔS > 0
Die Unordnung
nimmt so stark zu, dass insgesamt eine Energieabnahme möglich ist.
So
lösen sich Salze unter Abkühlung der Lösung auf.
|
|
|
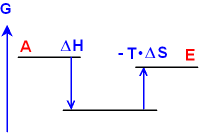
3
|
ΔS < 0, also Ordnung wird erzeugt.
(Das
scheint im Widerspruch zum "Gesetz 1" zu sein.)
ΔG < 0, wenn a) ΔH < 0 und
b)
| ΔH | > T | ΔS
|.
(Beachte:ΔS < 0 bedeutet - T ΔS
> 0!)
Ordnung kann erzeugt werden, wenn dafür die Enthalpie genügend
kleiner wird.
Nach diesem Prinzip entstehen
in der Natur unter Energieaufwand die komplizierten Moleküle!
|
|
Zum Verständnis:
|
Ist es möglich, dass in einer (spontan ablaufenden) endothermen Reaktion
auch Ordnung geschaffen wird?
|
|
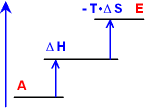
NEIN!
Endotherm ΔH
> 0;
Ordnung wird geschaffen,
d.h.
die Unordnung nimmt ab, ΔS < 0; damit - T ΔS
> 0;
Die Summe der zwei positiven Teile liefert ein ΔG
> 0; die Reaktion ist nicht möglich.
|
|
|
Ist es möglich, dass eine Reaktion zwar exotherm wäre - also nach
Berthelot möglich - aber tatsächlich nicht ablaufen kann?
|
|
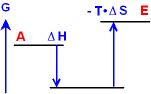
JA!
Exotherm
ΔH < 0;
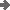damit ΔG >
0 muss der 2. Teil positiv und größer als der 1. Teil sein; -
T ΔS > |ΔH |;
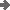ΔS
muss also gross und negativ sein (dann ist - T ΔS
groß und positiv);
Wenn bei der Reaktion sehr viel Ordnung entstehen
würde, kann die durch die Enthalpieabnahme zur Verfügung gestellte
Energie eventuell nicht mehr ausreichen.
|
|
|
Ist es möglich, dass eine Reaktion erst bei
hoher Temperatur ablaufen kann?
(Die Temperaturabhängigkeit
von ΔH und ΔS ist zu gering, um dies erklären zu können!)
|
|
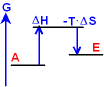
JA!
Die Lösung liegt
im obigen Fall Nr. 2 - endotherm mit Zunahme der Unordnung. Der 2. Teil der Gibbschen Gleichung enthält
T ΔS, also auch die Temperatur! Mit
zunehmender Temperatur wird daher der Betrag von T ΔS
größer!
|
|
T klein:
ΔG > 0
|
|
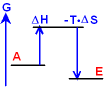
T groß:
ΔG
< 0
|
|
|
|
Anmerkung:
Bitte nicht verwechseln!
ΔG
legt fest, ob eine Reaktion möglich ist oder nicht.
Darin ist keine
Aussage über die Reaktionsgeschwindigkeit enthalten!
Die Reaktionsgeschwindigkeit
wird durch die Aktivierungsenergie bestimmt.
Enzyme verändern nicht ΔG,
sondern nur die Aktivierungsenergie.
Eine wegen ΔG
> 0 unmögliche Reaktion wird auch mit den besten Enzymen nicht möglich!
Anmerkung:
Bitte nicht verwechseln!
ΔG<0 ist
die Forderung für die Gesamtreaktion!
Eine Teilreaktion
kann auch ablaufen, wenn ΔG>0.
Dann ist
diese Teilreaktion mit einer anderen Reaktion gekoppelt. Die andere Reaktion
liefert genügend viel chemische Energie (ΔG<0),
dass die Teilreaktion Energie verbrauchen kann (ΔG>0)
und insgesamt immer noch die Reaktion möglich ist.
Die Energiespeicherung
in Organismen folgt diesem Prinzip. Durch Abbau von "Nährstoffen"
wird Energie gewonnen, die teilweise in anderen Substanzen gespeichert wird.
(Im nächsten Kapitel finden Sie ein quantitatives Beispiel dazu: der Abbau
von Glucose führt zur Energiespeicherung im Teilsystem ADP/ATP.)
|
|
Aus der Kenntnis von ΔG
sollten sich doch auch weitere Aussagen
zum Verhalten chemischer
Systeme machen lassen!
Allein die Angabe "eine Reaktion
ist möglich" ist recht wenig!
Ein kleiner Einblick
dazu.
(SCHWIERIGER!)
|
|
WEITER: Energiebilanz
bei der Verarbeitung der Glucose im Stoffwechsel