| Thermodynamik |
|||||
|
Temperaturabh. |
Tabelliert sind die Werte für
Standardbedingungen, aber natürlich ist eine Umrechung auf andere Bedingungen
möglich!
Der mathematische Formalismus
enthält (wie zu erwarten) die benötigten Formeln.
1. Gegeben sei eine Reaktionsenthalpie bei der Temperatur T1 ΔHR(T1); wie groß ist ΔHR(T2)?
|
Die Theorie liefert für ΔH die
Formel: |
|
|
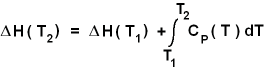
In nicht zu großen Temperaturintervallen ist CP
praktisch konstant, |
|
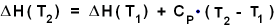
Diese Formeln gelten für jede Enthalpie, also auch für die Bildungsenthalpien ΔHB. Die Reaktionsenthalpie wurde als Summe "Produkte - Edukte" berechnet. In gleicher Weise kann man ein ΔCP berechen. Zu beachten ist, dass ΔHB für Elemente 0 ist, aber CP für Elemente nicht 0 ist. Allgemein folgt wieder eine Formel mit einem Integral.
|
Wenn temperaturunabhängige CP angenommen werden, gilt: |
|
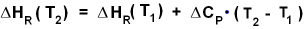
Vorher ("Beispiele") haben wir ΔHR für die
Reaktion CO + 1/2 O2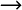 
CO2 unter Standardbedingungen (25 °C) berechnet: - 284 kJ/mol.
Welchen Wert berechnen wir für 300 °C? T2 - T1
= 300 - 25 = 275 °C = 375 K. (Temperaturdifferenzen sind in °C und K
gleich!).
Nach der Reaktionsgleichung ist ΔCP
= CP (CO2) - { CP(CO) + 1/2 * CP(O2)
}
Mit Tabellenwerten (Mittelwerte im Temperaturintervall) ist dies:
ΔCP
= 43 - { 32 + 1/2 * 31 } = 4,5 J K-1 mol-1.
Damit haben
wir: ΔHR (300
°C) = - 284 kJ / mol + 4,5 * 275 J / mol = -284 + 1,2 = -283 kJ /
mol.
{Alle Stoffe sind Gase, die sich ähnlich verhalten;
der Standardwert ist für diesen Fall in einem weiten Temperaturbereich
eine gute Näherung. Wenn nicht sehr präzise Angaben nötig sind,
sind die Rechnungen mit den Werten unter Standardbedingungen gut geeignet, um
das Reaktionsverhalten vorauszusagen.}
2. Die Druckabhängigkeit ist in der
Praxis kaum wichtig. Die Formel zeigt, dass für Gase in guter Näherung
die Druckabhängigkeit gering ist (für ideale Gase sogar exakt 0).
Wichtiger ist die Umrechnung auf andere Stoffmenge
als die Standardbedingung 1 mol. Und dies ist ein einfacher
Dreisatz!
Wenn für die Reaktion von 1 mol CO ΔHR
= - 284 kJ / mol, ist für z.B. 0,4 mol:
DHR
= 0,4 * (-284) = -133,6 kJ! (für 0,4 mol)
Anmerkung: Für die im 4. Kapitel eingeführten Größen S und G gibt es selbstständlich auch Formeln für die Umrechnung auf andere Temperaturen! Damit lässt sich das Verhalten von Stoffen und chemischen Reaktionen für jede Temperatur berechnen - "wie wir es von einer brauchbaren Theorie erwarten"!
ZURÜCK: Woher Sie gekommen sind - Bildungsenthalpie
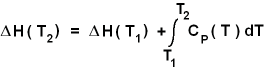
